多数元素

这题虽然是个简单题，但是官方给出的题解很丰富，我觉得可以通过这道题来拓展一下我们的解题思路

官方：169.多数元素 Leetcode官方题解

题目描述

给定一个大小为 n 的数组 nums ，返回其中的多数元素。多数元素是指在数组中出现次数大于 ⌊ n/2 ⌋ 的元素。

你可以假设数组是非空的，并且给定的数组总是存在多数元素。

示例 1：
输入：nums = [3,2,3]
输出：3

示例 2：
输入：nums = [2,2,1,1,1,2,2]
输出：2

提示：
n == nums.length
1 <= n <= 5 * 104
-109 <= nums[i] <= 109

进阶：尝试设计时间复杂度为 O(n)、空间复杂度为 O(1) 的算法解决此问题。

方法一：哈希表

思路
这是最容易想到的思路，使用哈希表记录每个元素出现的次数，只要某个元素次数出现超过n/2，那么这个元素就是众数。

算法
使用哈希表存储每个元素以及出现的次数。键表示一个元素，值表示这个元素出现的次数。循环遍历整个数组，只要有某一个数超过n/2，就返回这个数。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18


class Solution
{
  public:
    int majorityElement(vector<int> &nums)
    {
        unordered_map<int, int> map;
        int n = nums.size();
        for (int i = 0; i < n; i++)
        {
            map[nums[i]]++;
            if (map[nums[i]] > n / 2)
            {
                return nums[i];
            }
        }
        return 0;
    }
};

复杂度分析

时间复杂度：O(n)。其中 n 是数组 nums 的长度。我们遍历数组 nums 一次，对于 nums 中的每一个元素，将其插入哈希表都只需要常数时间。
空间复杂度：O(n)。哈希表中最多包含 n - (n/2) 个键值对。

方法二：排序

思路
如果将数组 nums 中的所有元素按照单调递增或单调递减的顺序排序，那么下标为[n/2]的元素（下标从 0 开始）一定是众数。

算法
对于这种算法，我们先将 nums 数组排序，然后返回上文所说的下标对应的元素。下面的图中解释了为什么这种策略是有效的。在下图中，第一个例子是 n 为奇数的情况，第二个例子是 n 为偶数的情况。

1
2
3
4
5
6
7
8
9


class Solution
{
  public:
    int majorityElement(vector<int> &nums)
    {
        sort(nums.begin(), nums.end());
        return nums[nums.size()/2];
    }
};

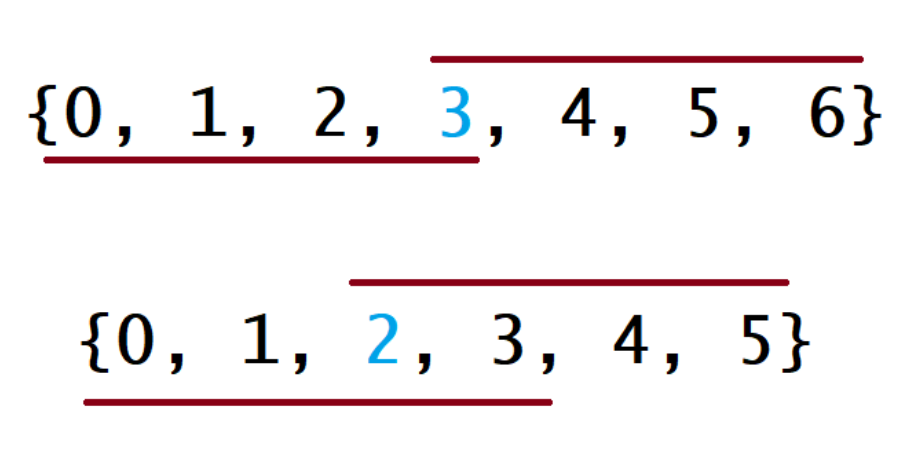
复杂度分析

时间复杂度：O(nlogn)。排序复杂度
空间复杂度：O(logn)。语言自带的排序算法需要使用O(logn)的栈空间。

方法三：随机化

思路
这个思路挺新颖的，因为众数占据超过一半的下标，所以有超过 50% 的概率能找到众数。

算法
由于一个给定的下标对应的数字很有可能是众数，我们随机挑选一个下标，检查它是否是众数，如果是就返回，否则继续随机挑选。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18


class Solution
{
  public:
    int majorityElement(vector<int> &nums)
    {
        while (true)
        {
            int candidate = nums[rand() % nums.size()];
            int count = 0;
            for (int num : nums)
                if (num == candidate)
                    ++count;
            if (count > nums.size() / 2)
                return candidate;
        }
        return -1;
    }
};

复杂度分析
时间复杂度：理论上最坏时间复杂度是O(∞)，运气很差的情况下一直得不到众数。但是众数占比超过 50% ，随机取数的概率还是非常大的。（这里我就没详细计算了，官方题解上有详细的计算）

空间复杂度：O(1)。随机方法只需要常数级别的额外空间

方法四：Boyer-Moore 投票算法

思路
如果使用一个变量count，初始化是0，遇到众数加1，反之减1，那么得到的count至少大于0。（因为众数最少都是n/2 + 1）

算法
维护一个候选众数 candidate 和出现次数count。初始时，candidate可以是任意数，count为0;
遍历整个nums，每次都判断当前数 num 是否等于candidate，相等则count增加，反之减少，每当count减小到负数，就更换candidate的值，count重置为0;
在遍历完成之后，candidate即为众数。

例子
简单的举一个例子：

nums	2	2	1	1	1	1	2	2	3	2	2	2	2
candidate	2	2	2	2	1	1	1	1	3	3	2	2	2
count	1	2	1	0	1	2	1	0	1	0	1	2	3

第一个数就是众数，假如我们使用value只记录众数 2 ，记录方法和count一样：

nums	2	2	1	1	1	1	2	2	3	2	2	2	2
value	1	2	1	0	-1	-2	-1	0	-1	0	1	2	3

你会惊讶的发现，此时的count和value要么相等，要么互为相反数，candidate是2时，就相等，candidate是其他数时，就互为相反数

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26


class Solution
{
  public:
    int majorityElement(vector<int> &nums)
    {
        int candidate = nums[0];
        int count = 0;
        for (auto num : nums)
        {
            if (num == candidate)
            {
                count++;
            }
            else
            {
                count--;
                if (count == 0)
                {
                    candidate = num;
                    count = 1;
                }
            }
        }
        return candidate;
    }
};

复杂度分析

时间复杂度：O(n)。值对数组进行一次扫描。
空间复杂度：O(n)。不需要额外的空间。

【面试高频】 169.多数元素

面试经典高频题型解题思路

多数元素

题目描述

方法一：哈希表

方法二：排序

方法三：随机化

方法四：Boyer-Moore 投票算法